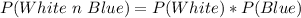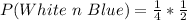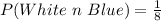Answer:
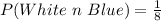
Explanation:
Given
Scarves: 1 green; 1 white
Hats: 1 blue; 1 red; 1 yellow; 1 purple
Required
Determine the probability of 1 blue hat and 1 white scarf
First, we need to determine the probability of blue hat
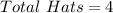
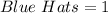
Hence;
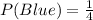
Next, we determine probability of white scarf
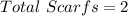
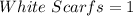
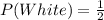
Calculating the required probability;