Question

Please help me to prove this!
I need is no.(c). So, please help me do it.
​

Answer 1

Answer: see proof below

Explanation:

Given: A + B + C = 90° → A + B = 90° - C

→ C = 90° - (A + B)

Use the Double Angle Identity: cos 2A = 1 - 2 sin² A

→ sin² A = (1 - cos 2A)/2

Use Sum to Product Identity: cos A + cos B = 2 cos [(A + B)/2] · cos [(A - B)/2]

Use the Product to Sum Identity: cos (A - B) - cos (A + B) = 2 sin A · sin B

Use the Cofunction Identities: cos (90° - A) = sin A

sin (90° - A) = cos A

Proof LHS → RHS:

LHS: sin² A + sin² B + sin² C

`\text{Double Angle:}\qquad (1-\cos 2A)/(2)+(1-\cos 2B)/(2)+\sin^2 C\\\\\\.\qquad \qquad \qquad =(1)/(2)\bigg(2-\cos 2A-\cos 2B\bigg)+\sin^2 C\\\\\\.\qquad \qquad \qquad =1-(1)/(2)\bigg(\cos 2A+\cos 2B\bigg)+\sin^2 C`

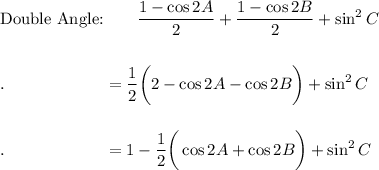
`\text{Sum to Product:}\quad 1-(1)/(2)\bigg[2\cos \bigg((2A+2B)/(2)\bigg)\cdot \cos \bigg((2A-2B)/(2)\bigg)\bigg]+\sin^2 C\\\\\\.\qquad \qquad \qquad =1-\cos (A+B)\cdot \cos (A-B)+\sin^2 C`

Given: 1 - cos (90° - C) · cos (A - B) + sin² C

Cofunction: 1 - sin C · cos (A - B) + sin² C

Factor: 1 - sin C [cos (A - B) + sin C]

Given: 1 - sin C[cos (A - B) - sin (90° - (A + B))]

Cofunction: 1 - sin C[cos (A - B) - cos (A + B)]

Sum to Product: 1 - sin C [2 sin A · sin B]

= 1 - 2 sin A · sin B · sin C

LHS = RHS: 1 - 2 sin A · sin B · sin C = 1 - 2 sin A · sin B · sin C
`\checkmark`