Answer:
The statement that describes a situation that can be modeled as a growth or decay over equal interval is;
C. A species of fly doubles its population every month during the summer
Explanation:
We have for exponential growth or decay, the following equation;
Exponential growth or decay;
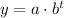
Where;
a = The initial amount of the item
1 + r = The rate of growth in percentage
b = The growth or decay factor
t = The time
For exponential decay, we have;
0 < b < 1
b = 1 - r

For exponential growth, we have;
b > 1
b = 1 + r
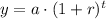
Therefore, given that the number of the fly population doubles every month, we have the growth rate, r as 100%, which is written as 100/100 = 1, to give;
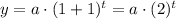
Which is expressed as an exponential growth by an equal factor of, r, over equal intervals of, t, time.