Question

Solve this equation and show your work! (1 point for the correct answer and 1 point for showing how to solve the equation) x³ = -2,197

Answer 1

Make the 3 into a fraction and then flip it to cancel out which makes it easier then do it to the -2,197 for you to get x

Answer 2

Here we are given with a equation:

`{x}^(3) = - 2197`

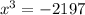
And we have to solve it with appropriate steps.

So, let's start solving.

Add 2197 to both sides of the equation,

`{x}^(3) + 2197 = - 2197 + 2197`

`{x}^( 3) + 2197 = 0`

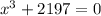
Now, using the identity:

• a³ + b³ = (a + b)(a² - ab + b²)

Let's proceed further.

x³ is the cube of x and 2197 is the cube of 13

`(x) {}^(3) + (13) {}^(3) = 0`

`(x + 13)( {x}^(2) - x * 13 + {13}^(2) ) = 0`

`(x + 13)( {x}^(2) - 13x + 13) = 0`

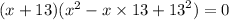
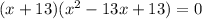
Now,

• x + 13 = 0
• x² - 13x + 13 = 0

So, x = -13

And, for the second let's use the discriminate formula,

➝ D = b² - 4ac

➝ D = (-13)² - 4(1)(13)

➝ D = 169 - 52

➝ D = 117

Now, using the D. formula,

`x = ( - b \pm √( D) )/(2a)`

`x = (13 \pm √(117) )/(2)`

`x = (13 \pm 3 √(13) )/(2)`

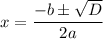
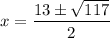
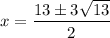
So the roots of the equation are:

`{ \boxed{ \bf{x = - 1 ,\: (13 + 3 √(13) )/(2) and \: (13 - 3 √(13) )/(2) }}}`

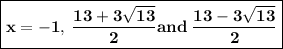
And we are done !!

#CarryOnLearning

━━━━━━━━━━━━━━━━━━━━