Question

A technician compares repair costs for two types of microwave ovens (type I and type II). He believes that the repair cost for type I ovens is greater than the repair cost for type II ovens. A sample of 61 type I ovens has a mean repair cost of $79.60, with a standard deviation of $23.47. A sample of 45 type II ovens has a mean repair cost of $75.25, with a standard deviation of $15.07. Conduct a hypothesis test of the technician's claim at the 0.05 level of significance. Let μ1 be the true mean repair cost for type I ovens and μ2 be the true mean repair cost for type II ovens.Step 3 of 4 : Determine the decision rule for rejecting the null hypothesis H0. Round the numerical portion of your answer to three decimal places.

Answer 1

The question is missing some parts. Here is the complete question.

A technician compares repair costs for two types of microwave ovens (type I and type II). He believes that the repair cost for type I ovens is greater than the repair cost in type II ovens. A samplle of 61 type I ovens has a mean repair cost of $79.60, with a standard deviation of $23.47. A sample of 45 type II ovens has a mean repair cost of $75.25, with standar deviation of $15.07. Conduct a hypothesis test of the technician's claim at the 0.05 level of significance. Let
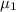`\mu_(1)` be the true mean repair cost for type I ovens and
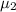`\mu_(2)` be the true mean repair cost for type II ovens.

Step 1 of 4: State null and alternative hypothesis for the test.

Step 2 of 4: Compute the value of test statistics. Round your answer to 2 decimal places.

Step 3 of 4: Determine the decision rule for rejecting the null hypothesis. Round the numerical portion of your answer to 3 decimal places.

Step 4 of 4: Make the decision for the hypothesis test. (Reject or fail to reject Null Hypothesis)

Answer and Step-by-step explanation:

First, state null and alternative hypothesis:

`H_(0): \mu_(1)=\mu_(2)`

`H_(a): \mu_(1)>\mu_(2)`

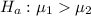
Use z-statistics:

`z = (x_(1)-x_(2))/(y)`

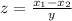
where x₁ and x₂ are the means and:

`y=\sqrt{(s_(1)^(2))/(n_(1))+(s_(2)^(2))/(n_(2)) }`

Calculating value of test stattistic:

`y=\sqrt{((23.47)^(2))/(61)+(75.25^(2))/(45) }`

`y = √(9.030+5.046)`

`y = √(14.076)`

y = 3.752

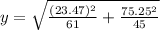
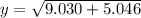
`z = (79.6-75.25)/(3.752)`

z = 1.16

The test statistics is z = 1.16

The decision rule for rejecting null hypothesis is:
`\alpha` ≤ test statistics

Using z-score table, it is possible to determine p-value, which is:

p-value = 0.877

Comparing p-value with level of significance (α = 0.05):

0.877 > 0.05

Therefore, we fail to reject the null hypothesis.