Answer:
Z score=2.46.
Explanation:
The Z score for sample mean $31,650 can be computed by using following formula

Here, sample mean=xbar=31650
population standard deviation=sigma=3339
population mean=29056
and sample size=n=10.

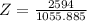
Z=2.4567
Z=2.46 (rounded to two decimal places).
Hence the resultant z-score is 2.46.