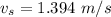Question

A trumpet player on a moving railroad flatcar moves toward a second trumpet player standing alongside the track both play a 490 Hz note. The sound waves heard by a stationary observer between the two players have a beat frequency of 2.0 beats/s. What is the flatcar's speed? Take the speed of sound to be 343 m/s.

Answer 1

The value is
`v_s = 1.394 \ m/s`

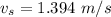
Step-by-step explanation:

From the question we are told that

The frequency of the second player is
`f_2 = 490 \ Hz`

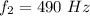
The beat frequency is
`f_b = 2.0 \ Hz`

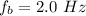
The speed of sound is
`v_s = 343 \ m/s`

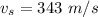
Generally the frequency of the note played by the first player is mathematically represented as

`f_1 = f_2 + f_b`

=>
`f_1 = 490 + 2.0`

=>
`f_1 = 492 Hz`

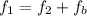
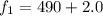
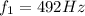
From the relation of Doppler Shift we have that

`f_1 = ( f_2 (v+ v_o ))/(v-v_s )`

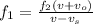
Here
`v_o\ is\ the\ velocity\ of\ the\ observer\ with\ value\ 0 \ m/s`

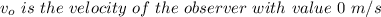
So

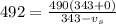
`492 = ( 490 (343+0 ))/(343 -v_s )`

=>
`v_s = 1.394 \ m/s`