The question is incomplete. Here is the complete question.
To understand the decibel scale. The decibel scale is a logarithmic scale for measuring the sound intensity level. Because the decibel scale is logarithmic, it changes by an additive constant when the intensity when the intensity as measured in W/m² changes by a multiplicative factor. The number of decibels increase by 10 for a factor of 10 increase in intensity. The general formula for the sound intensity level, in decibels, corresponding to intensity I is
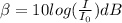 ,
,
where
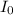 is a reference intensity. for sound waves,
is a reference intensity. for sound waves,
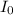 is taken to be
is taken to be
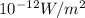 . Note that log refers to the logarithm to the base 10.
. Note that log refers to the logarithm to the base 10.
Part A: What is the sound intensity level β, in decibels, of a sound wave whose intensity is 10 times the reference intensity, i.e.
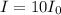 ? Express the sound intensity numerically to the nearest integer.
? Express the sound intensity numerically to the nearest integer.
Part B: What is the sound intensity level β, in decibels, of a sound wave whose intensity is 100 times the reference intensity, i.e.
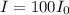 ? Express the sound intensity numerically to the nearest integer.
? Express the sound intensity numerically to the nearest integer.
Part C: Calculate the change in decibels (
 and
and
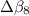 ) corresponding to f = 2, f = 4 and f = 8. Give your answer, separated by commas, to the nearest integer -- this will give an accuracy of 20%, which is good enough for sound.
) corresponding to f = 2, f = 4 and f = 8. Give your answer, separated by commas, to the nearest integer -- this will give an accuracy of 20%, which is good enough for sound.
Answer and Explanation: Using the formula for sound intensity level:
A)
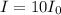

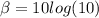
β = 10
The sound Intensity level with intensity 10x is 10dB.
B)
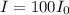
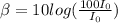
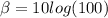
β = 20
With intensity 100x, level is 20dB.
C) To calculate the change, take the f to be the factor of increase:
For
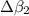 :
:
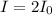
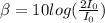
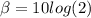
β = 3
For
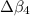 :
:
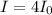
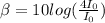
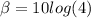
β = 6
For
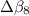 :
:

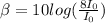
β = 9
Change is
 ,
,
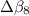 = 3,6,9 dB
= 3,6,9 dB