Answer:
1) The exergy of destruction is approximately 456.93 kW
2) The reversible power output is approximately 5456.93 kW
Step-by-step explanation:
1) The given parameters are;
P₁ = 8 MPa
T₁ = 500°C
From which we have;
s₁ = 6.727 kJ/(kg·K)
h₁ = 3399 kJ/kg
P₂ = 2 MPa
T₂ = 350°C
From which we have;
s₂ = 6.958 kJ/(kg·K)
h₂ = 3138 kJ/kg
P₃ = 2 MPa
T₃ = 500°C
From which we have;
s₃ = 7.434 kJ/(kg·K)
h₃ = 3468 kJ/kg
P₄ = 30 KPa
T₄ = 69.09 C (saturation temperature)
From which we have;
h₄ =
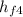 + x₄×
+ x₄×
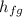 = 289.229 + 0.97*2335.32 = 2554.49 kJ/kg
= 289.229 + 0.97*2335.32 = 2554.49 kJ/kg
s₄ =
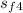 + x₄×
+ x₄×
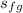 = 0.94394 + 0.97*6.8235 ≈ 7.563 kJ/(kg·K)
= 0.94394 + 0.97*6.8235 ≈ 7.563 kJ/(kg·K)
The exergy of destruction,
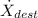 , is given as follows;
, is given as follows;
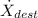 = T₀ ×
= T₀ ×
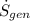 = T₀ ×
= T₀ ×
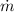 × (s₄ + s₂ - s₁ - s₃)
× (s₄ + s₂ - s₁ - s₃)
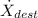 = T₀ ×
= T₀ ×
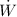 ×(s₄ + s₂ - s₁ - s₃)/(h₁ + h₃ - h₂ - h₄)
×(s₄ + s₂ - s₁ - s₃)/(h₁ + h₃ - h₂ - h₄)
∴
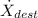 = 298.15 × 5000 × (7.563 + 6.958 - 6.727 - 7.434)/(3399 + 3468 - 3138 - 2554.49) ≈ 456.93 kW
= 298.15 × 5000 × (7.563 + 6.958 - 6.727 - 7.434)/(3399 + 3468 - 3138 - 2554.49) ≈ 456.93 kW
The exergy of destruction ≈ 456.93 kW
2) The reversible power output,
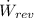 =
=
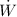 +
+
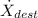 ≈ 5000 + 456.93 kW = 5456.93 kW
≈ 5000 + 456.93 kW = 5456.93 kW
The reversible power output ≈ 5456.93 kW.