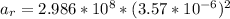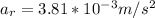Answer:
The value is
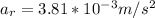
Step-by-step explanation:
Generally the moon's radial acceleration is mathematically represented as

Here
 is the angular velocity which is mathematically represented as
is the angular velocity which is mathematically represented as
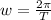
substituting
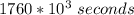 for T(i.e the period of the moon ) we have
for T(i.e the period of the moon ) we have

=>
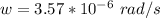
From the question r(which is the radius of the orbit ) is evaluated as
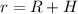
substitute
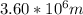 for R and
for R and
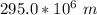 H
H
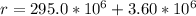
=>
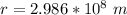
So