Question

A rectangular box with a depth of 10 inches and a square base is to be manufactured by the Bold Box Company. The top of the box costs $1.20 per square inch, the bottom costs $.95 per square inch and the sides cost $.75 per square inch. Express the cost of manufacturing this box as a function of length.

Answer 1

The cost function of manufacturing this box is:

`C_(T) = 2.15\cdot x^(2)+30\cdot x`, where
`x` is the length of the box, measured in US dollars.

Explanation:

From the statement we know that:

1) The box has a square base (
`w = l = x`).

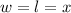2) The box has a depth of 10 inches (
`h = 10\,in`).

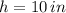3) The cost of manufacturing the top of the box is $ 1.20 per square inch.

4) The cost of manufacturing the bottom of the box is $ 0.95 per square inch.

5) The cost of manufacturing each side of the box is $ 0.75 per square inch.

The total cost of manufacturing the box is:

`C_(T) =C_(bottom) + C_(top) + 4\cdot C_(side)`

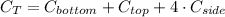
Where:

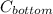`C_(bottom)` - Cost of the bottom of the box, measured in US dollars.

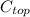`C_(top)` - Cost of the top of the box, measured in US dollars.

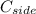`C_(side)` - Cost of the side of the box, measured in US dollars.

Dimensionally, cost equals unit cost, measured in US dollars by square inch, multiplied by surface area, measured in square inches. Now, the expression is expanded:

`C_(T) = c_(bottom)\cdot x^(2)+c_(top)\cdot x^(2)+4\cdot c_(side)\cdot h\cdot x`

`C_(T) =(c_(bottom)+c_(top))\cdot x^(2)+4\cdot c_(side)\cdot h \cdot x`

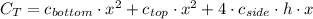
If we know that
`c_(bottom) = \$\,0.95\,in^(-2)`,
`c_(top) = \$\,1.20\,in^(-2)`,
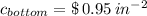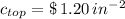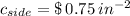`c_(side) = \$\,0.75\,in^(-2)` and
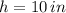`h = 10\,in`, the cost function of manufacturing this box is:

`C_(T) = 2.15\cdot x^(2)+30\cdot x`, where
`x` is the length of the box, measured in US dollars.