Answer:
x(t) = 581.66 lb
Explanation:
From the given information:
Consider the salt quantity in the tank at time t be x(t) lb.
∴ the rate of change of salt content in the tank is
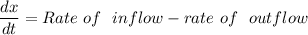
where:
the rate of inflow = salt conc. × flow rate = 3 lb/gallon × 7 gallons
=21 lb/s
rate of outflow = salt conc. in the tank × flow rate
= x/250 × 9
= 9x/250 lb/s
∴
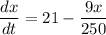
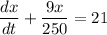
This is a 1st order linear differentiation,
The integrating factor if
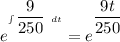
∴
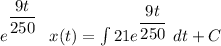
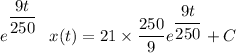
 at t = (0) and x(0) = 100 lb
at t = (0) and x(0) = 100 lb
Hence;
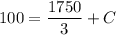
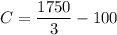
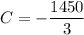
∴

after time t = 1 minute i.e 60 s
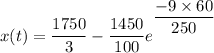

x(t) = 581.66 lb