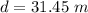Question

ou are walking down a straight path in a park and notice there is another person walking some distance ahead of you. The distance between the two of you remains the same, so you deduce that you are walking at the same speed of 1.05 m/s. Suddenly, you notice a wallet on the ground. You pick it up and realize it belongs to the person in front of you. To catch up, you start running at a speed of 2.75 m/s. It takes you 18.5 s to catch up and deliver the lost wallet. How far ahead of you was this person when you started running

Answer 1

The value is
`d = 31.45 \ m`

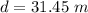
Step-by-step explanation:

Generally the relative speed at which you are moving with respect to the person ahead of you is mathematically represented as

`v_r = v_s - v_c`

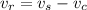
substituting 1.05 m/s for
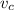`v_c` and 2.75 m/s for
`v_s`

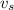
So

`v_r = 2.75 - 1.05`

=>
`v_r = 1.7 \ m/s`

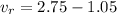
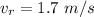
Generally the distance by which the person is ahead of you is mathematically represented as

`d = v_r * t`

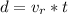
substituting 18.5 s for
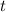
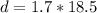
`t`

`d =  1.7  * 18.5`

=>
`d  =  31.45 \  m`