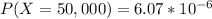Question

Suppose that the number of miles that an EV battery (electric vehicle) can run before its battery wears out is exponentially distributed with the average value of 100,000 miles. If a car manufacturer decides to install this type of battery to power the vehicle, do the following: 1) What percentage of the cars will fail at the end of 50,000 miles

Answer 1

The value is
`P(X = 50,000) = 6.07*10^(-6)`

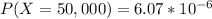
Explanation:

From the question we are told that

The average value is
`E(x) = 100000 \ miles`

Generally the exponential distribution function is mathematically represented as

`f(x) = \{ \left \theta* e^(-\theta * x ) \ ; \ \ \theta >0} \atop {0 \ ; \ otherwise }} \right.`

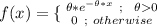
Here
`\theta` is a constant which is mathematically represented as

`\theta = (1)/(E(x))`

=>
`\theta = (1)/(100000)`

=>
`\theta =1 *10^(-5)`

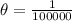
So at x = 50,000 miles (given)

`f(50000) = 1 *10^(-5) * e^{-1*10^(-5) * 50000}`

`f(50000) = 6.07*10^(-6)`

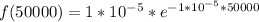
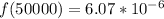
So the percentage of the cars will fail at the end of 50,000 miles is

`P(X = 50,000) = 6.07*10^(-6)`