Question

Suppose a fast-pitch softball player does a windmill pitch, moving her hand through a circular arc with her arm straight. She releases the ball at a speed of 21.3 m/s21.3 m/s (about 47.6 mph47.6 mph ). Just before the ball leaves her hand, the ball's radial acceleration is 871 m/s2871 m/s2 . What is the length of her arm from the pivot point at her shoulder?

Answer 1

Step-by-step explanation:

linear speed of ball v = 21.3 m /s

radial acceleration = 871 m /s²

radial acceleration = v² / R

where R is length of arm which acts as radius of circular path of the ball .

Putting the values

21.3² / R = 871

R = .52 m.

Answer 2

R = 52.08 cm

Step-by-step explanation:

given data

tangential velocity v = 21.3 m/s

radial acceleration aR = 871 m/s²

solution

we will get here length of her arm from the pivot point at her shoulder so

here we know aR =
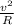`(v^2)/(R)` ........................1

so put here value and we get

871 =
`(21.3^2)/(R)`

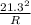
R = 0.5208840 m

R = 52.08 cm