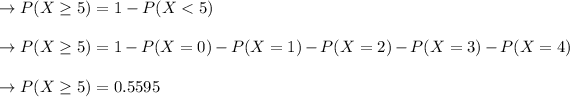Answer:
The answer to this question can be defined as follows:
In option a "0.0067".
In option b "0.1755".
In option c "0.5595".
Explanation:
It is about the distribution of Poisson:

t = 1
The formula for calculating Mean:
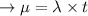
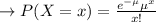
calculate the value of Mean:
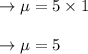
In point a:
When the value of x is equal to 0:
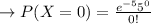
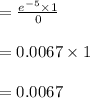
In point b:
When the value of x is equal to 5:
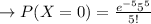

In point c:
When the value of x is equal to 5: