Question

A standardized​ exam's scores are normally distributed. In a recent​ year, the mean test score was and the standard deviation was . The test scores of four students selected at random are ​, ​, ​, and . Find the​ z-scores that correspond to each value and determine whether any of the values are unusual.

Answer 1

The following are the solution to this question:

Explanation:

In the given question, some of the values are missing which is defined in the attached file please find it.

In this question, the data is used to represent a standardized​ exam's scores, which is normally spread out into the test score that is 1530 and its standard deviation 316.

Formula:

`\to z=(X- \mu)/(\sigma ) \\`

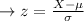
If the value of z-score= 1930

`\to z =(1930- 1530)/(316 ) \\\\ \to z =(400)/(316 ) \\\\ \to z = 1.27`

The z-score is 1.27

If the value of z-score= 1250

`\to z =(1250- 1530)/(316 ) \\\\ \to z =(-280)/(316 ) \\\\ \to z = -0.886`

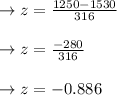
The z-score is -0.886

If the value of z-score= 2250

`\to z =(2250- 1530)/(316 ) \\\\ \to z =(720)/(316 ) \\\\ \to z = 2.27`

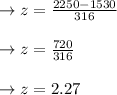
The z-score is = 2.27

If the value of z-score= 1420

`\to z =(1420- 1530)/(316 ) \\\\ \to z =(-110)/(316 ) \\\\ \to z = -0.348`

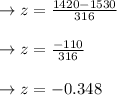
The z-score is = -0.348