Answer: The mean and standard error of the sampling distribution of sample proportions are 0.40 and 0.0219 respectively.
Explanation:
Formula : Mean of the sampling distribution of sample proportions

Standard error of the sampling distribution of sample proportions
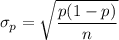
, where p = population proportion
n= sample size
Here, p =0040
n= 500
So , Mean of the sampling distribution of sample proportions
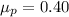
Standard error of the sampling distribution of sample proportions
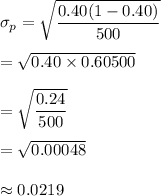
Hence, mean and standard error of the sampling distribution of sample proportions are 0.40 and 0.0219 respectively.