Question

One of the most spectacular and least known hummingbirds is the Marvelous Spatuletail, Loddigesia mirabilis, found in only in a single remote valley in northern Peru (see photo below). In this valley the mean density is 3 spatuletails per 100-hectare quadrat. (a) What is the probability a random quadrat contains less than 3 spatuletails

Answer 1

P(x < 3) = 0.42319

Explanation:

From the given information:

The mean density
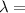`\lambda =` 3

Let x be the random variable that follows a Poisson distribution.

Therefore:

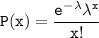`\mathtt{P(x) = (e^(-\lambda) \lambda ^x)/(x!)}` for x =1, 2, 3...

However, the probability that a random quadrat contains less than 3 spatuletails can be computed as:

`\mathtt{P(x <3 ) = (e^(-3)3 ^0)/(0!)+ (e^(-3)3 ^1)/(1!)+ (e^(-3) 3 ^2)/(2!) }`

`\mathtt{P(x <3 ) =e^(-3) \begin{pmatrix} (3 ^0)/(0!)+ (3 ^1)/(1!)+ (3 ^2)/(2!) \end {pmatrix} }`

`\mathtt{P(x <3 ) =e^(-3) \begin{pmatrix} (1)/(1)+ (3 )/(1)+ (9)/(2) \end {pmatrix} }`

`\mathtt{P(x <3 ) =e^(-3) \begin{pmatrix} 1+3+ 4.5 \end {pmatrix} }`

`\mathtt{P(x <3 ) =e^(-3) \begin{pmatrix}8.5 \end {pmatrix} }`

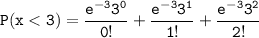
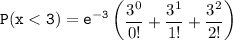
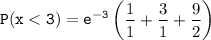
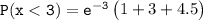
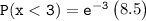
P(x < 3) = 0.42319