Question

If an angle of a parallelogram is two-third of

its adjacent angle, the smallest angle of the
parallelogram is
(a) 54°
(b) 72°
(c) 81°
(d) 108°

Answer 1

We know that in a parallelogram two opposite angles are equal -

`\\ \implies \sf \: 2x + 2y = 360 {}^( \circ) \\ \\ \\ \implies \sf \: x + y = 180 {}^( \circ) \qquad \quad \: (i) \\`

Given -

• angle x is equal to the two - third of it's adjacent angle y.

`\\ \implies \sf \: x = (2)/(3) y \\ \\ \\ \implies \sf (x)/(2) = (y)/(3) = k \\ \\ \\ \qquad \sf \small \underline{ x = 2k \: \: \& \: \: y = 3k} \\`

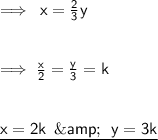
Now, by using equation (1) :

`\\ \implies \sf \: 2k + 3k = 180 \\ \\ \\ \implies \sf \: 5k = 180 \\ \\ \\ \implies \sf \: k = (180)/(5) \\ \\ \\ \large{ \boxed{ \sf{k = {36}^( \circ) }}} \\`

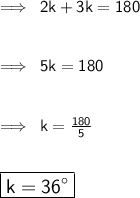
Now, by putting the value of k in x and y.

• x = 2k = 2 × 36 = 72°
• y = 3k = 3 × 36 = 108°

Therefore, the right option and smallest angle is b) 72°.