Question

Help asap please!! <3

Answer 1

y = -2x + 4 or y = -2(x - 2)

Explanation:

Equation of Line AB

• y = mx + c

1. m = slope
2. c = y-intercept

Finding slope (m)

• m = -2 - 6 / 3 + 1
• m = -8/4
• m = -2

Finding c using point slope equation

• c - 6 = -2(0 + 1)
• c - 6 = -2
• c = 4

Equation

• Line AB : y = -2x + 4 or y = -2(x - 2)

Answer 2

The easiest way to do this is to put the line into slope intercept form. This is equal to y = mx + b, where m is the slope and y is the intercept. I'm assuming the point at which the line intercepts the y axis is at (0, 4) The graph isn't numbered, so its hard to tell.

Assuming b = 4, we need to find m

Slope = rise / run

Or

`m = (y_2 - y_1)/(x_2 - x_1) \\`

Substitute -2 for y2, 6 for y1, 3 for x2 and -1 for x1

`m = (-2 - 6)/(3 - -1)\\ m = (-8)/(4)\\m = -2`

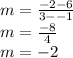
Plug these values in and

`y = -2x + 4`

When you graph this on desmos, the two points (-1, 6) and (3, -2) are on the graph. Therefore, I'm assuming the y intercept was in fact 4 :)