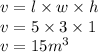Question

Help me please thank u

Answer 1

`225 {m}^(3)`

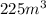
Explanation:

To find the volume of the shape first we have to split the shape into two rectangles; a large one at the bottom and a small one at the top. The formula to find volume of a rectangle is

`v = length * width * height`

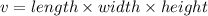
note that after both volumes are found they should be added to determine the volume of the entire shape*

The length of the large rectangle is 5m, the width is 7m, and the height is 6m. Therefore the volume is

`v = l * w * h \\ v = 5 * 7 * 6 \\ v = 210 {m}^(3)`

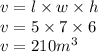
The length of the small rectangle is 5m, the width is 3m, and the height is 1m. Therefore the volume is

`v = l * w * h \\ v = 5 * 3 * 1 \\ v = 15 {m}^(3)`

`210 {m}^(3) + 15 {m}^(3) = 225 {m}^(3) \\ therefore \: the \: volume \: of \: the \: \\ entire \: shape \: is: \\ 225 {m}^(3)`

Answer 2

`V_(\ total)=225\ m^3`

Explanation:

Step 1: Find the volume of the big box

`V_(\ big) = l * w * h`

`V_(\ big) = 7\ m * 5\ m * 6\ m`

`V_(\ big) = 210\ m^3`

Step 2: Find the volume of the small box

`V_(\ small) = l * w * h`

`V_(\ small) = 3\ m * 5\ m * (7\ m - 6\ m)`

`V_(\ small) = 3\ m * 5\ m * 1\ m`

`V_(\ small) = 15\ m^3`

Step 3: Combine the volumes

`V_(\ total)=V_(\ big) + V_(\ small)`

`V_(\ total)=210\ m^3 + 15\ m^3`

`V_(\ total)=225\ m^3`

Answer:
`V_(\ total)=225\ m^3`