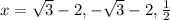Question

Solve 2x^3+7x^2-2x-1=o​

Answer 1

`x=√(3)-2\\x=-√(3)-2\\x=(1)/(2)`

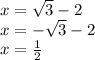
Explanation:

This is a hard one

We have to use the rational root theorem

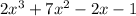`2x^3+7x^2-2x-1` = 0

We have to find all the factors of a and d and put them in a fraction

`a=2\\d=-1\\(1)/(1,2)`

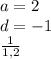
We then plug them into the equation to see if any of them work

The equation isn't true when plugging 1, but is true when plugging in 1/2

factored form of 1/2 is (2x-1)

Then we divide the original equation by (2x-1) (you can use synthetic division or long division, it would be hard to type out the process for that) to get
`x^2+4x+1`

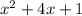
So now the equation is
`(2x-1)(x^2+4x+1)`

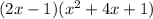
Solve the second half of this equation using the quadratic formula to get

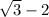`√(3)-2` and
`-√(3)-2`

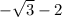
We already know the solution for the first half of the equation (1/2)

So the final answers are:

`x=√(3)-2, -√(3)-2, (1)/(2)`