Question

If the half-life of iodine-131 is 8.0 days, how much of a 100.0 mg sample of it will remain after 32 days? In case you're interested, iodine-131 forms xenon-131 by beta emission/decay. Please enter only a numerical answer and do not write in any units. It is understood that the unit is mg.

Answer 1

Given :

Half-life of Iodine ,
`t_(0.5)=8 \ days` .

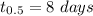Initial concentration ,
`[A_o]=100\ mg` .

To Find :

The amount of sample remains after 32 days .

Solution :

Rate constant is given by :

`k=(0.693)/(t_(0.5))\\\\k=(0.693)/(8)\ s^(-1)\\\\k=0.086625\ s^(-1)`

Now , by rate law :

`[A]=[A_o]e^(-kt)`

Putting all given values, we get :

`[A]=100* e^(-(0.086625)* 32)\\`

`[A]=6.25\ mg`

Therefore , the remaining sample after 32 days is 6.25 mg .

Hence , this is the required solution .