Answer:

Explanation:
 :
:
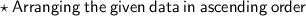 :
:
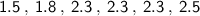
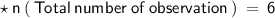
Finding the position of median

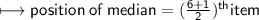
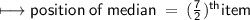
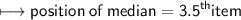
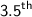 item is the average of 3rd and 4th items.
item is the average of 3rd and 4th items.
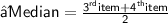



∴ Median = 2.3
-------------------------------------------------------------
▪️If n is odd , the median is the value of the
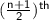 observation.
observation.
▪️If n is even, the median is the average of
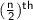 and
and
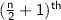 observation.
observation.
Hope I helped!
Best regards! :D
~TheAnimeGirl