Answer:
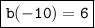
Explanation:
We are given the function:

We want to find b(-10). Therefore, we must plug -10 in for each x.
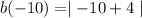
Solve inside of the absolute value symbol. Add 4 to -10 ⇒ -10+4= -6
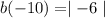
Absolute value represents how far away a number is from 0. It is always positive.
-6 is 6 away from 0. Therefore, the absolute value of -6 is 6.
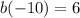
b(-10) is equal to 6.