Question

Solve: 3(2x+1)-2(x-5)-5(5-2x)=16 value of x?​

Answer 1

`\boxed{ \bold{ \huge{ \boxed{ \sf{x = 2}}}}}`

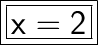
Explanation:

`\displaystyle{ \star{ \: \: \underline{ \sf{given \: equation}}}}` :

`\sf{3(2x + 1) - 2(x - 5) - 5(5 - 2x) = 16}`

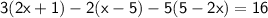
Distribute 3 through the parentheses

`\mapsto{\sf{6x + 3- 2(x - 5)- 5(5 -2x) = 16}}`

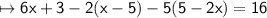
Distribute 2 through the parentheses

`\mapsto{ \sf{6x + 3 - 2x + 10- 5(5 - 2x) = 16}}`

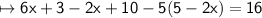
Distribute 5 through the parentheses

`\mapsto{ \sf{6x + 3 - 2x + 10 - 25 + 10x = 16}}`

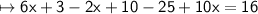
Combine ike terms and simplify it

Like terms are those which have the same base

`\mapsto{ \sf{6x - 2x + 10x + 3 + 10 - 25 = 16}}`

`\mapsto{ \sf{4x + 10x + 3 + 10 - 25 = 16}}`

`\mapsto{ \sf{14x + 3 + 10 - 25 = 16}}`

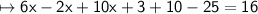
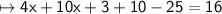
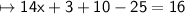
Add the numbers : 3 and 5

`\mapsto{ \sf{14x + 13 - 25 = 16}}`

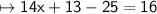
The negative and positive integers are always subtracted but posses the sign of the bigger integer.

`\mapsto{ \sf{14x - 12 = 16}}`

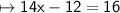
Move 17 to right hand side and change it's sign

`\mapsto{ \sf{14x = 16 + 12}}`

Add the numbers: 16 and 17

`\mapsto{ \sf{14x = 28}}`

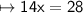
Divide both sides by 14

`\mapsto{ \sf{ (14x)/(14) = (28)/(14)}}`

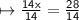
Calculate

`\mapsto{ \boxed{ \sf{x = 2}}}`

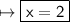
The value of x is 2

Hope I helped!

Best regards!

~TheAnimeGirl