Question

What is the value of x?
30
45
55
60​

Answer 1

In the diagram, we can see that two lines are intersecting and a two pairs of vertically opposite angles are forming. The angle on a line are supplementary to each other (linear pair).

• Supplementary angles add upto 180°.

Here, angle TRS and angle TRV are linear pair, so they will have a sum of 180°.

Then,

`\angle TRS + \angle TRV = 180 \degree`

In the question, given angle TRS = x and angle TRV = 3x

`x + 3x = 180 \degree`

`4x = 180 \degree`

Now, divide 4 from both sides because we need to find x.

`x = (180 \degree)/(4)`

`x = 45 \degree`

It was given that Angle TRS is x

So, Angle TRS = 45°

Option B

#CarryOnLearning

━━━━━━━━━━━━━━━━━━━━

Answer 2

`\boxed {\tt B. \ x=45}`

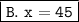
Explanation:

x and 3x are on a straight line together. Therefore, they are supplementary and must add to 180 degrees.

Add x and 3x, and set that equal to 180.

`x+3x=180`

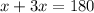
Combine like terms on the right side of the equation. Both x and 3x have a variable, so they can be added together.

`(x+3x)=180`

`4x=180`

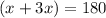
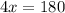
Since we want to find x, we have to isolate x. x is being multiplied by 4. The inverse of multiplication is division. Divide both sides of the equation by 4.

`(4x)/(4) =(180)/(4)`

`x=(180)/(4)`

`x=45`

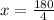
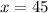
x is equal to 45, so the correct answer is B. 45