Answer:
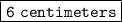
Explanation:
The volume of a cube can be found using the following formula:
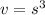
where
 is the side length, or edge.
is the side length, or edge.
We know the volume is 216 cubic inches. We can substitute 216 cm³ in for
 , the volume.
, the volume.
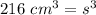
We want to find the side length. Therefore, we must isolate the variable,
 .
.
s is being cubed. The inverse of a cube is the cube root. Take the cube root of both sides of the equation.
![\sqrt[3]{216 \ cm^3} =\sqrt[3]{s^3}](https://img.qammunity.org/2021/formulas/mathematics/high-school/di6a180ijzmiazd2vzre33ow19elb0ozyh.png)
![\sqrt[3]{216 \ cm^3} =s](https://img.qammunity.org/2021/formulas/mathematics/high-school/2gmujfuz83i3recfig16e21qwpmxdha5e0.png)
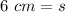
The length of each edge of the cube is 6 centimeters.