Question

1. In how many ways can a committee of eight people to be formed from a group of 6 male, 5 female and 4 students if there are no restrictions, as all members are eligible?

Answer 1

The number of ways is 6435

Explanation:

Given

`Male = 6`

`Female = 5`

`Students = 4`

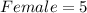
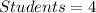
Required

Number of ways a group of 8 can be formed

Here, I'll assume each category of people are distinct:

Hence;

`Total = Male + Female + Students`

`Total = 6 + 5 + 4`

`Total = 15`

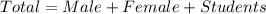
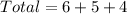
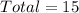
Number of ways is then calculated as follows:

`^nC_r = (n!)/((n - r)!r!)`

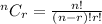
Where

`n = 15\ and\ r = 8`

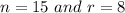
So, we have:

`^(15)C_8 = (15!)/((15 - 8)!8!)`

`^(15)C_8 = (15!)/(7! * 8!)`

`^(15)C_8 = (15 * 14 * 13 * 12 * 11 * 10 * 9 * 8!)/(7!8!)`

`^(15)C_8 = (15 * 14 * 13 * 12 * 11 * 10 * 9)/(7!)`

`^(15)C_8 = (15 * 14 * 13 * 12 * 11 * 10 * 9)/(7 * 6 *5 * 4 * 3 * 2 * 1)`

`^(15)C_8 = (32432400)/(5040)`

`^(15)C_8 = 6435`

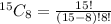
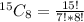
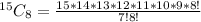
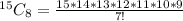
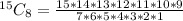
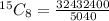
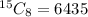
Hence, the number of ways is 6435