Answer:
K(8, 4)
Explanation:
Given:
M(2, 1), P(12, 6)
MK:KP = 3:2
Required:
Coordinates of K
SOLUTION:
Coordinates of K can be determined using the formula below:
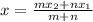
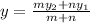
Where,
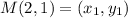
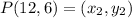
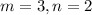
Plug in the necessary values to find the coordinates of K:
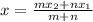
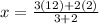
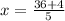
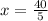
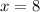
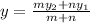
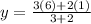
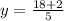
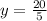
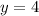
The coordinates of K = (8, 4)