Question

The quadratic function h(t) = -16.1? + 150 models a ball's height, in feet, over time, in seconds,

after it is dropped from a 15 story building.

From what height in feet, was the ball dropped?

After how many seconds, rounded to the nearest hundredth, did the ball hit the ground?

Answer 1

Hello!

The answer is: The first graphic representation.

Why?

We are given a quadratic equation, meaning that it could be two possible solutions for the exercise, however, we are talking about time, so we have to consider only the obtained positive values.

Let's make the equation equal to 0 in order to find the values of "t"

`h(t) = -16.1t^2 + 150`

`0=-16.1t^2+150`

`16.1t^2=150`

`t^2=(150)/(16.1) =9.32`

`t=+-√(9.32) =+-3.05`

`t1=3.05`

`t2=-305`

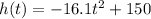
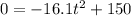
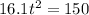
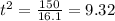
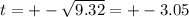
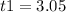
So, discarding the negative value, we can use the possitive value to find the correct graphic representation.

To find the correct graphic representation we must take into consideration the following:

- We must remember that the sign of the coefficient of the quadratic term (t^2) will define if the parabola opens downward or upward.

From the given quadratic (or parabola) equation we have:

`a=-1`

`b=0`

`c=150`

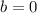
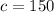
So, since the coefficient of the quadratic term is negative, the parabola opens downward.

- Since we are looking for a graphic that represents the change in height over time, we need to look for a graphic that shows only positive values for the x-axis (time)

- We are looking for a parabola which y-axis intercept is equal to 150.

Therefore, the graphic representation of the quadratic function that models a ball's height over time is the first graphic representation.

Have a nice day!