Question

How do you do this problem?

Answer 1

Your answer is absolutely correct

Explanation:

The work would be as follows:

`\int _0^(√(\pi ))4x^3\cos \left(x^2\right)dx,\\\\\mathrm{Take\:the\:constant\:out}:\quad \int a\cdot f\left(x\right)dx=a\cdot \int f\left(x\right)dx\\=> 4\cdot \int _0^(√(\pi ))x^3\cos \left(x^2\right)dx\\\\\mathrm{Apply\:u-substitution:}\:u=x^2\\=> 4\cdot \int _0^(\pi )(u\cos \left(u\right))/(2)du\\\\\mathrm{Apply\:Integration\:By\:Parts:}\:u=u,\:v'=\cos \left(u\right)\\=> 4\cdot (1)/(2)\left[u\sin \left(u\right)-\int \sin \left(u\right)du\right]^(\pi )_0\\\\`

`\int \sin \left(u\right)du=-\cos \left(u\right)\\=> 4\cdot (1)/(2)\left[u\sin \left(u\right)-\left(-\cos \left(u\right)\right)\right]^(\pi )_0\\\\\mathrm{Simplify\:}4\cdot (1)/(2)\left[u\sin \left(u\right)-\left(-\cos \left(u\right)\right)\right]^(\pi )_0:\quad 2\left[u\sin \left(u\right)+\cos \left(u\right)\right]^(\pi )_0\\\\\mathrm{Compute\:the\:boundaries}:\quad \left[u\sin \left(u\right)+\cos \left(u\right)\right]^(\pi )_0=-2\\=> 2(-2) = - 4`

Hence proved that your solution is accurate.

Answer 2

`\int\limits^(√(\pi))_0 {4x^3\cos(x^2)} \, dx=-4`

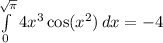
Explanation:

So we have the integral:

`\int\limits^(√(\pi))_0 {4x^3\cos(x^2)} \, dx`

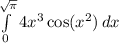
As told, let's use u-substitution first and then use integration by parts.

For the u-substitution, we can let u to be equal to x². So:

`u=x^2`

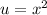
Differentiate:

`du=2x\, dx`

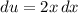
We can rewrite our integral as:

`\int\limits^(√(\pi))_0 {2x(2x^2)\cos(x^2)} \, dx`

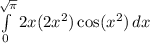
Therefore, by making our u-substitution, our integral is now:

`\int\limits {2u\cos(u)} \, du`

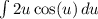
We also need to change our bounds. Substitute them into u. So:

`u=√(\pi)^2=\pi\\u=(0)^2=0`

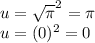
Therefore, our integral with our new bounds is:

`\int\limits^(\pi)_(0) {2u\cos(u)} \, du`

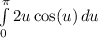
Now, let's use integration by parts. Integration by parts is given by:

`\int\limits {v}\, dy=vy-\int y\, dv`

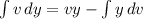
(I changed the standard u to y because we are already using u).

Let's let v be 2u and let's let dy be cos(u). Thus:

`v=2u\\dv=2\,du`

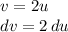
And:

`dy=\cos(u)\\y=\sin(u)`

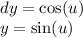
So, do integration by parts:

`=2u\sin(u)-\int \sin(u)2\,du`

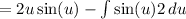
Simplify:

`=2u\sin(u)-2\int \sin(u)\,du`

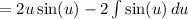
Evaluate the integral:

`=2u\sin(u)+2\cos(u)`

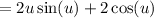
Now, use the bounds. So:

`(2(\pi)\sin(\pi)+2\cos(\pi))-(2(0)\sin(0)+2\cos(0))`

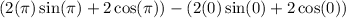
Evaluate:

`=(2\pi(0)+2(-1))-(0(0)+2(1))`

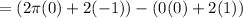
Simplify:

`=(-2)-(2)`

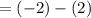
Subtract:

`=-4`

And we're done!