Answer:
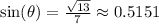
Explanation:
So we know that Θ is acute and that:
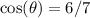
First, note that since Θ is acute, it is between 0 and 90 degrees, meaning that all of our trig ratios will be positive since the angle is in the Quadrant I.
The Pythagorean Identity is:
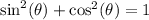
We know that cosine is 6/7. Substitute:
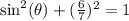
Square:
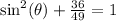
Subtract both sides by 36/49. Change the 1 to 49/49 to make a common denominator:
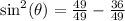
Subtract:
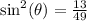
Take the square root of both sides:
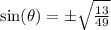
Simplify:
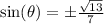
As mentioned previously, since Θ is acute, all of the trig functions must be positive. So, we can ignore our negative answer:
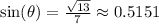
and we're done!