Answer:
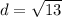
Explanation:
Use the Distance Formula to help you determine the distance between the two following points:
-Distance Formula:
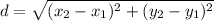
(where
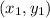 represents the first point and
represents the first point and
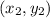 represents the second point)
represents the second point)
-Apply the two following points onto that equation:
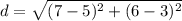

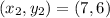
-Solve the equation:
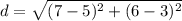
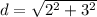
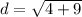
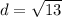
So therefore, the distance is
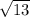 .
.