Answer:
The tensions in
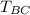 is approximately 4,934.2 lb and the tension in
is approximately 4,934.2 lb and the tension in
 is approximately 6,035.7 lb
is approximately 6,035.7 lb
Step-by-step explanation:
The given information are;
The angle formed by the two rope segments are;
The angle, Φ, formed by rope segment BC with the line AB extended to the center (midpoint) of the ship = 26.0°
The angle, θ, formed by rope segment BD with the line AB extended to the center (midpoint) of the ship = 21.0°
Therefore, we have;
The tension in rope segment BC =
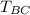
The tension in rope segment BD =

The tension in rope segment AB =
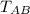 = Pulling force of tugboat = 1200 lb
= Pulling force of tugboat = 1200 lb
By resolution of forces acting along the line A_F gives;
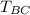 × cos(26.0°) +
× cos(26.0°) +
 × cos(21.0°) =
× cos(21.0°) =
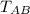 = 1200 lb
= 1200 lb
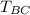 × cos(26.0°) +
× cos(26.0°) +
 × cos(21.0°) = 1200 lb............(1)
× cos(21.0°) = 1200 lb............(1)
Similarly, we have for equilibrium, the sum of the forces acting perpendicular to tow cable = 0, therefore, we have;
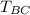 × sin(26.0°) +
× sin(26.0°) +
 × sin(21.0°) = 0...........................(2)
× sin(21.0°) = 0...........................(2)
Which gives;
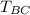 × sin(26.0°) = -
× sin(26.0°) = -
 × sin(21.0°)
× sin(21.0°)
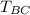 = -
= -
 × sin(21.0°)/(sin(26.0°)) ≈ -
× sin(21.0°)/(sin(26.0°)) ≈ -
 × 0.8175
× 0.8175
Substituting the value of,
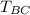 , in equation (1), gives;
, in equation (1), gives;
-
 × 0.8175 × cos(26.0°) +
× 0.8175 × cos(26.0°) +
 × cos(21.0°) = 1200 lb
× cos(21.0°) = 1200 lb
-
 × 0.7348 +
× 0.7348 +
 ×0.9336 = 1200 lb
×0.9336 = 1200 lb
 ×0.1988 = 1200 lb
×0.1988 = 1200 lb
 ≈ 1200 lb/0.1988 = 6,035.6938 lb
≈ 1200 lb/0.1988 = 6,035.6938 lb
 ≈ 6,035.6938 lb
≈ 6,035.6938 lb
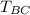 ≈ -
≈ -
 × 0.8175 = 6,035.6938 × 0.8175 = -4934.1733 lb
× 0.8175 = 6,035.6938 × 0.8175 = -4934.1733 lb
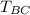 ≈ -4934.1733 lb
≈ -4934.1733 lb
From which we have;
The tensions in
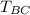 ≈ -4934.2 lb and
≈ -4934.2 lb and
 ≈ 6,035.7 lb.
≈ 6,035.7 lb.