Question

Find the perimeter P of ▱JKLM with vertices J(−3,−2), K(−5,−5), L(1,−5), and M(3,−2). Round your answer to the nearest tenth, if necessary.

Answer 1

Given:

Vertices of JKLM are J(−3,−2), K(−5,−5), L(1,−5), and M(3,−2).

To find:

The perimeter P of a parallelogram JKLM.

Solution:

Distance formula:

`D=√((x_2-x_1)^2+(y_2-y_1)^2)`

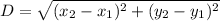
Using distance formula, we get

`JK=√(\left(-5-\left(-3\right)\right)^2+\left(-5-\left(-2\right)\right)^2)`

`JK=√(\left(-5+3\right)^2+\left(-5+2\right)^2)`

`JK=√(\left(-2\right)^2+\left(-3\right)^2)`

`JK=√(4+9)`

`JK=√(13)`

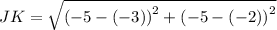
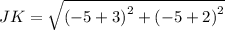
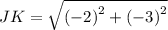
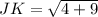
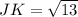
Similarly,

`KL=√(\left(1-\left(-5\right)\right)^2+\left(-5-\left(-5\right)\right)^2)=6`

`LM=√(\left(3-1\right)^2+\left(-2-\left(-5\right)\right)^2)=√(13)`

`JM=√(\left(3-\left(-3\right)\right)^2+\left(-2-\left(-2\right)\right)^2)=6`

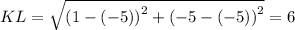
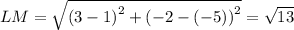
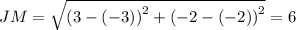
Now, perimeter P of ▱JKLM is

`P=JK+KL+LM+JM`

`P=√(13)+6+√(13)+6`

`P=2√(13)+12`

`P=2(3.61)+12`

`P=7.22+12`

`P=19.22`

`P\approx 19.2`

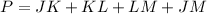
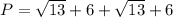
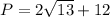
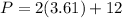
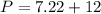
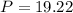
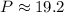
Therefore, the perimeter P of ▱JKLM is 19.2 units.