2 Answers

Drew Hunter · Answer 1 · 2021-09-26T06:53:16+0000

Answer:

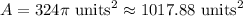
$A=324\pi \text{ units}^2\approx1017.88\text{ units}^2$

Explanation:

The formula for arc length is:

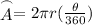
$\stackrel{\frown}{A}=2\pi r((\theta)/(360)})$

Where Θ is measured in degrees.

We know that the arc length is 8π when the degree is 80. So, substitute 8π for A and 80 for Θ:

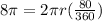
$8\pi=2\pi r((80)/(360))$

Divide both sides by 2π:

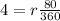
4=r(80)/(360)

Simplify the fraction:

4=(2)/(9)r

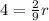
Multiply both sides by 9/2:

r=18

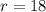
So, the radius is 18.

Now, we can find the area of the circle. The formula for the area of a circle is:

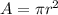
$A=\pi r^2$

Substitute 18 into r:

$A=\pi (18)^2$

Simplify:

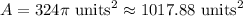
$A=324\pi \text{ units}^2\approx1017.88\text{ units}^2$

And we're done!

Please log in or register to add a comment.