Answer:
Tanya is 14; Ruby is 11.
Explanation:
Let T represent Tanya's current age and let R represent Ruby's current age.
We know that their ages add up to 25. So:
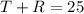
8 years ago, Tanya was twice as old as Ruby. In other words, Tanya's current age minus 8 is the same as Ruby's current age minus 8 times 2. So:
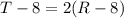
We have a system of equations. We can solve by substitution. From the first equation, subtract R from both sides:
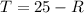
Substitute this into the second equation:
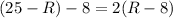
On the left, subtract. On the right, distribute:

Add 16 to both sides. The right side cancels:
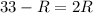
Add R to both sides. The left cancels:

Divide both sides by 3:
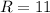
So, Ruby is currently 11 years old.
So, Tanya is currently 25-11 or 14 years old.
Check:
8 years ago, Ruby was 11-8 or 3 years old.
8 years ago, Tanya is 14-8 or 6 years old.
Tanya's age of 6 is 2 times Ruby's age of 3 so our answer is correct.