Question

B. How tar from the li u

b. Obtain the value of g from the motion of the moon assuming that its period
of rotation round the earth is 27 days 8 hours and the radius of its orbit is
60.1 times the radius of the earth.
0.
7.2 m. Compute​

Answer 1

Approximately
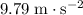`9.79\; \rm m \cdot s^(-2)` at the surface of the earth, given that the radius of the earth is known to be approximately
`6.371* 10^(6)\; \rm m`. Assumptions: the earth is a sphere, the orbit of the moon is circular, and that the gravitational pull of the earth is the only force on the moon.

Step-by-step explanation:

Convert the orbital period of the moon around the earth to seconds:

`\begin{aligned}t &= (27\; \text{day} * 24\; \text{hours} \cdot \text{day}^(-1) + 8\; \text{hour})* 3600\; \rm \text{s}\cdot \text{hour}^(-1)\\ &= 2361600\; \text{s} \end{aligned}`.

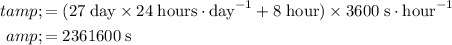Calculate the angular velocity of the moon around the earth using the formula
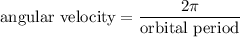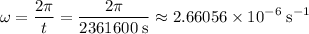`\displaystyle \text{angular velocity} = \frac{2\pi}{\text{orbital period}}`:

`\begin{aligned}\omega = (2\pi )/(t) = (2\pi)/(2361600\; \rm s) \approx 2.66056* 10^(-6)\; \rm s^(-1)\end{aligned}`.

Let
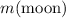`m(\text{moon})` denote the mass of the moon. Let
`g` denote the gravitational field strength at the surface of the earth (not at the position of the moon.) Let
`r` denote the radius of the earth.

The orbital radius of the moon would thus be
`60.1\, r`. Note that in the gravitational field due to a single spherical mass, the field strength is inversely proportional to the square of distance from the center of that mass.

• The surface of the earth is at a distance of
  `r` away from the center of the earth.
• The distance between the moon and the center of the earth would then be
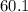  `60.1` times that number (that is:
  `60.1\, r`.)

The gravitational field at the surface of the earth is
`g`. Therefore, at the position of the moon (
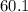`60.1` times further away from the center of the earth compared to the earth surface,) the gravitational field strength would be:

`\displaystyle \left( (r^2)/((60.1\, r)^2) \right)\, g = (g)/(60.1^2)`,

Hence, the gravitational pull of the earth on the moon would be
`\displaystyle \frac{m(\text{moon})\, g}{60.1^2}`.

Assume that the gravitational pull of the earth is the only force on the moon. That gravitational pull would then be the equal (in size) to the net force on the moon. That is:

`\displaystyle \text{Net force on the moon} = \frac{m(\text{moon})\, g}{60.1^2}`.

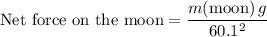On the other hand, the rotation (assumed to be perfectly circular) of the moon would give the net force on the moon in terms of:

• the mass of the moon,
• the angular speed of the rotation, and
• the radius of the orbit.

`\displaystyle \text{Net force on the moon} = m(\text{moon})\, \omega^2\, (60.1\, r)`.

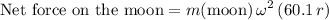Combine the two expressions for the net force on the moon to obtain an equation for
`g`:

`\displaystyle \frac{m(\text{moon})\, g}{60.1^2} = m(\text{moon})\, \omega^2\, (60.1\, r)`.

Simplify and solve for
`g`:

`\displaystyle g = 60.1^3 \, \omega^2\, r`.

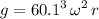The angular velocity of this rotation,
`\omega`, has already been found to be approximately
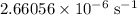`2.66056* 10^(-6)\; \rm s^(-1)`. Look up the radius of the earth:
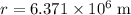`r = 6.371* 10^(6)\; \rm m`. Evaluate this expression for
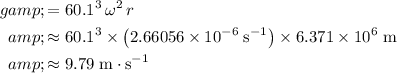`g`:

`\begin{aligned}g &= 60.1^3 \, \omega^2\, r \\ &\approx 60.1^3 * \left( 2.66056* 10^(-6)\; \rm s^(-1)\right) * 6.371* 10^(6)\;\rm m \\ &\approx 9.79\; \rm m \cdot s^(-1)\end{aligned}`.