Because this is a linear problem, I'd use the slope-intercept formula:

where
m = slope (rise/run)
y = dependent value
x = independent value
b = constant value
Because the plumber charges $17 upon arrival, it is our constant. The $36 is our slope (per hour, per minute, per etc. is generally a give away). Additionally because the total cost of the plumber's visit depends on how long s/he stays at a client's home, the $89 is our y value. Therefore the equation should look like this:
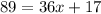
Solve for x by subtracting 17 from both sides of the equation then dividing by 36.
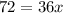
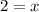
The plumber spent two hours at his/her client's home.