Question

I need this TONIGHT!!! Three years ago, Jolene bought $750 worth of stock in a software company. Since then the value of her purchase has been increasing at an average rate of 5 1/2% per year. How much is the stock worth now? (Round each money calculation you make to the nearest cent.) The stock is worth $ now.

Answer 1

Formula: A = P(1 + r/n)^t

We have these variables:

P = 750

r/n = 0.055

t = 3

Substitute and simplify:

A = 750(1 + 0.055)^3

A = 750(1.055)^3

A = 880.68

Best of Luck!

Answer 2

`A\approx\$880.68`

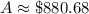
Explanation:

So, we know that Jolene bought an initial $750.

We also know that the purchase is increasing at an average rate of 5 1/2 %or 5.5%. In other words, this is being compounded.

So, we can use the compound interest formula, which is:

`A=P(1+(r)/(n))^(nt)`

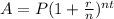
Where A is the total amount, P is the principal value, r is the rate and n is the number of times compounded per year, and t is the amount of years.

So, substitute 750 for P. 5 1/2% is the same as 5.5% or 0.055 (you move the decimal two places to the left and remove the percent symbol) so substitute this for r. Since it's increasing yearly, n is 1. So, our formula is:

`A=750(1+0.055)^t`

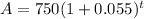
Add:

`A=750(1.055)^t`

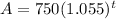
Since the stock was bought 3 years ago, the value now is t=3. So, substitute 3 for t and evaluate:

`A=750(1.055)^3`

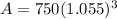
Evaluate. Use a calculator:

`A\approx\$880.68`

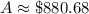
And we're done!