Answer:
The center of this circle is at
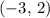 . The radius of this circle is
. The radius of this circle is
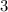 .
.
Explanation:
A circle with center
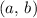 and a radius of
and a radius of
 (
(
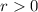 ) could be expressed as:
) could be expressed as:
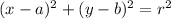 .
.
(In other words, a point is on this circle if and only if the distance between that point and the center is equal to the radius.)
Rearrange this equation using binomial expansion to match the equation given in this question:
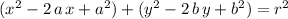 .
.
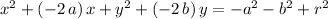 .
.
The equation in this question is:
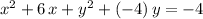 .
.
Match up the coefficients of
 and
and
 in the two equations.:
in the two equations.:
- Coefficient of
 :
:
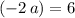 .
. - Coefficient of
 :
:
 .
.
Thus,
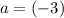 and
and
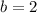 .
.
The constants of the two equations should also match up:
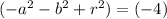 .
.
Substitute in
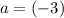 as well as
as well as
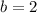 and solve for
and solve for
 :
:
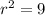 .
.
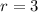 (since
(since
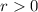 .)
.)
Therefore, the center of this circle is
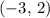 . The radius of this circle is
. The radius of this circle is
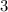 .
.