Question

May you please answer question #9

Answer 1

Answer: Approximately 0.78388 seconds

==========================================

Explanation:

Plug in t = 0 to find that

h = -16t^2 - 64t + 60

h = -16(0)^2 - 64(0) + 60

h = 60

The starting height is 60 feet.

-----

Now plug in h = 0 and solve for t.

h = -16t^2 - 64t + 60

0 = -16t^2 - 64t + 60

-16t^2 - 64t + 60 = 0

From here use the quadratic formula

`t = (-b\pm√(b^2-4ac))/(2a)\\\\t = (-(-64)\pm√((-64)^2-4(-16)(60)))/(2(-16))\\\\t = (64\pm√(7936))/(-32)\\\\t = (64+√(7936))/(-32) \ \text{ or } \ t = (64-√(7936))/(-32)\\\\t \approx -4.78388 \ \text{ or } \ t \approx 0.78388 \\\\`

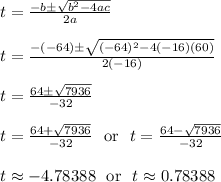
We ignore the negative t value as a negative time doesn't make sense.

The only practical answer is roughly t = 0.78388 seconds.