Question

Una piscina rectangular de 15 metros de largo por 9 metros de ancho està rodeada por un

camino de cemento de ancho uniforme. Si el área del camino es 112 metros cuadrados, ¿cuánto
mide su ancho?

Answer 1

Answer: 2 meters.

Explanation:

Let w = width of the cement path.

Dimensions of pool : Length = 15 meters , width = 9 meters

Area of pool = length x width = 15 x 9 = 135 square meters

Along width cement path, the length of region =
`2w+15`

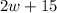
width =
`2w+9`

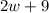
Area of road with pool =
`(2w+15) (2w+9)`

`= 4w^2+30w+18w+135\\\\=4w^2+48w+135`

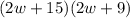
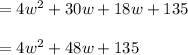
Area of road = (Area of road with pool ) -(area of pool)

`\Rightarrow\ 112 =4w^2+48w+135- 135\\\\\Rightarrow\ 112= 4w^2+48w\\\\\Rightarrow\ 4 w^2+48w-112=0\\\\\Rightarrow\ w^2+12w-28=0\ \ \ [\text{Divide both sides by 4}]\\\\\Rightarrow\ w^2+14w-2w-28=0\\\\\Rightarrow\ w(w+14)-2(w+14)=0\\\\\Rightarrow\ (w+14)(w-2)=0\\\\\Rightarrow\ w=-14\ or \ w=2`

width cannot be negative, so w=2 meters

Hence, the width of the road = 2 meters.