Question

without building the graph, find the coordinates of the point of intersection of the lines given by the equation y=3x-1 and 3x+y=-7

Answer 1

1. Determining the value of x and y:

Given equation(s):

• 
  `y = 3x - 1`
• 
  `3x + y = -7`

To determine the point of intersection given by the two equations, it is required to know the x-value and the y-value of both equations. We can solve for the x and y variables through two methods.

Method-1: Substitution method

Given value of the y-variable: 3x - 1

Substitute the given value of the y-variable into the second equation to determine the value of the x-variable.

`\implies 3x + y = -7`

`\implies3x + (3x - 1) = -7`

`\implies3x + 3x - 1 = -7`

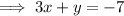
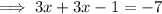
Combine like terms as needed;

`\implies 3x + 3x - 1 = -7`

`\implies 6x - 1 = -7`

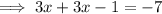
Add 1 to both sides of the equation;

`\implies 6x - 1 + 1 = -7 + 1`

`\implies 6x = -6`

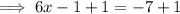
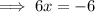
Divide 6 to both sides of the equation;

`\implies (6x)/(6) = (-6)/(6)`

`\implies x = -1`

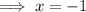
Now, substitute the value of the x-variable into the expression that is equivalent to the y-variable.

`\implies y = 3(-1) - 1`

`\implies`
`\ \ = -3 - 1`

`\implies`
`= -4`

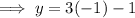
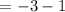
Therefore, the value(s) of the x-variable and the y-variable are;

`\boxed{x = -1}`
`\boxed{y = -4}`

Method 2: System of equations

Convert the equations into slope intercept form;

`\implies\left \{ {{y = 3x - 1} \atop {3x + y = -7}} \right.`

`\implies \left \{ {{y = 3x - 1} \atop {y = -3x - 7}} \right.`

Clearly, we can see that "y" is isolated in both equations. Therefore, we can subtract the second equation from the first equation.

`\implies \left \{ {{y = 3x - 1 } \atop {- (y = -3x - 7)}} \right.`

`\implies \left \{ {{y = 3x - 1} \atop {-y = 3x + 7}} \right.`

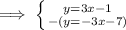
Now, we can cancel the "y-variable" as y - y is 0 and combine the equations into one equation by adding 3x to 3x and 7 to -1.

`\implies\left \{ {{y = 3x - 1} \atop {-y = 3x + 7}} \right.`

`\implies 0 = (6x) + (6)`

`\implies0 = 6x + 6`

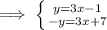
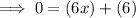
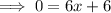
This problem is now an algebraic problem. Isolate "x" to determine its value.

`\implies 0 - 6 = 6x + 6 - 6`

`\implies -6 = 6x`

`\implies -1 = x`

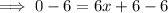
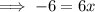
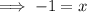
Like done in method 1, substitute the value of x into the first equation to determine the value of y.

`\implies y = 3(-1) - 1`

`\implies y = -3 - 1`

`\implies y = -4`

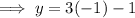
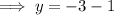
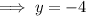
Therefore, the value(s) of the x-variable and the y-variable are;

`\boxed{x = -1}`
`\boxed{y = -4}`

2. Determining the intersection point;

The point on a coordinate plane is expressed as (x, y). Simply substitute the values of x and y to determine the intersection point given by the equations.

⇒ (x, y) ⇒ (-1, -4)

Therefore, the point of intersection is (-1, -4).

Graph: