Question

Which linear equation below represents the line that goes through the point (3.4) and has a slope of 2?

Answer 1

Linear equation with a slope of 2 that goes through the point (3, 4) is
`y = 2\cdot x -2`.

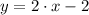Explanation:

From statement we know the slope of the line and a point contained in it. Using the slope-point equation of the line is the quickest approach to determine the appropriate equation, whose expression is:

`y-y_(o) = m \cdot (x-x_(o))`

Where:

`m` - Slope, dimensionless.

`x_(o)`,
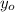`y_(o)` - Components of given point, dimensionless.

`x`,
`y` - Independent and dependent variable, dimensionless.

If we know that
`m = 2`,
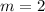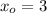`x_(o) = 3` and
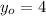`y_(o) = 4`, the linear equation is found after algebraic handling:

1)
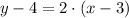`y-4 = 2\cdot (x-3)` Given

2)
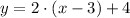`y = 2\cdot (x-3) +4` Compatibility with Addition/Existence of Additive Inverse/Modulative Property

3)
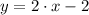`y = 2\cdot x -2` Distributive Property/
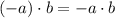`(-a)\cdot b = -a\cdot b`/Definition of sum/Result

Linear equation with a slope of 2 that goes through the point (3, 4) is
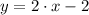`y = 2\cdot x -2`.