Answer:
(a) , . and .
(b)
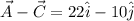 .
.
(c)
 and the direction
and the direction
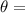 124.56°.
124.56°.
Step-by-step explanation:
Given that,
,
and

(a) The magnitude of a vector is the square root of the sum of the square of all the components of the vector, i.e. for a ,.
So, the magnitude of the is
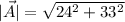
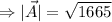
.
The magnitude of the is
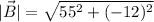
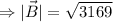
.
And, the magnitude of the is
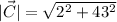
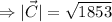
.
(b) The difference between the two vectors is the difference between the corresponding components of the vectors. So, the required expression of is

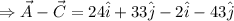

(c) The expression of is
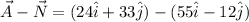
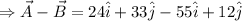
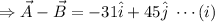
The magnitude of is

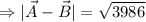
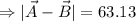
Now, if a vector
 in 3rd quadrant having direction
in 3rd quadrant having direction
 with respect to
with respect to
 direction, than
direction, than
in the anti-clockwise direction.
Here, from equation (i), for the vector
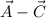 ,
,
 and
and
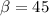 .
.
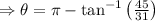
180°-55.44° [as \pi radian= 180°]
124.56° in the anti-clockwise direction.
(d) Vector diagrams for
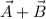 and
and
 has been shown
has been shown
in the figure(b) and figure(c) recpectively.
Vector
 is in 3rd quadrant as calculated in part (c).
is in 3rd quadrant as calculated in part (c).
While Vector
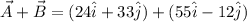
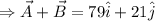 , which is in 1st quadrant as both the components are position has been shown in figure(b).
, which is in 1st quadrant as both the components are position has been shown in figure(b).