Question

Line segment JK in the coordinate plane has endpoints with coordinates \left(-4,11\right)(−4,11) and \left(8,-1\right)(8,−1).Supposed J, P, and K are collinear on segment JK, and JP:JK=\frac{1}{3}JP:JK=1/3 . What are the coordinates of P?

Answer 1

(-1, 8)

Explanation:

Given P to be the point that divides the coordinates J and K in the ratio 1:3

then the coordinate of point P will be xpressed as;

P(X, Y) =
`((bx_1+ax_2)/(b+a), (by_1+ay_2)/(b+a))`

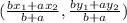
Given J = (-4, 11) and K = (8, -1)

`x_1 = -4, y_1 = 11, x_2 = 8 \ and \ y_2 = -1, a = 1, b = 3`

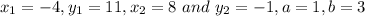
substituting the given parameters into the line division formula

`P(X, Y) = ((3(-4)+1(8))/(3+1), (3(11)+(1)(-1))/(3+1))\\\\P(X, Y) = ((-12+8)/(4), (33-1)/(4))\\\\P(X, Y) = ((-4)/(4), (32)/(4))\\\\P(X, Y) = (-1, 8)`

Hence the coordinates of P is (-1, 8)