Answer:
It is a perfect cube with sides of 5.
Explanation:
If 125 was a perfect square, there would be a whole number A which, squared, would give us 125.
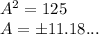
We can see that the roots are not whole numbers.
(Tip: without a calculator, we can find this by testing
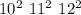 to see if any give us 125. We get 100, 121, 144 respectively. None of them is 125.)
to see if any give us 125. We get 100, 121, 144 respectively. None of them is 125.)
If it was a perfect cube, there would be a whole number B which, cubed, would give us 125.
![B^3 = 125\\B = \sqrt[3]{125} \\B = 5](https://img.qammunity.org/2021/formulas/mathematics/college/kujo8zrdjzks9kbg30ofp657ak54l0d4w1.png)
As we can see, there IS a whole number B: 5 !
(Without a calculator, like the previous one, we could try
 and we'd find that
and we'd find that
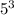 = 125)
= 125)
Answer: It is a perfect cube with sides of 5.